Normalverteilungen

Darstellung einer Normalverteilung basierend auf ermittelten Parametern

Bisher haben wir im Kurs uns darauf konzentriert, Parameter wie Mittelwert oder Standardabweichung für Werte einer Stichprobe zu berechnen. Oftmals interessiert uns jedoch die Grundgesamtheit, und in den kommenden Wochen werden wir uns konkret damit beschäftigen.

Dazu müssen in einem ersten Schritt jedoch kennenlernen, wie man eine Normalverteilung darstellt, wenn die Parameter Mittelwert und Standardabweichung bekannt sind. Die grundsätzliche Idee dabei ist:

Erstellung (Simulation) von x-Werten, dem sog. Wertebereich
Berechnung der y-Werte für die x-Werte. Dabei folgen die y-Werte einer Normalverteilung mit \(\overline{x}\) und \(\sigma\)

Erstellung des Wertebereichs

Hier nutzen wir die Funktion seq(), die wir bereits in Woche 1 kennengelernt haben:

x_werte <- seq(0, 50, 0.1)

Der Vektor x-Werte enthält hier alle Werte zwischen 0 und 50 in Intervallen von 0.1

Berechnung der Normalverteilung mittels `dnorm`

Nun berechnen wir die zu x_werte gehörenden y-Werte, unter der Annahme, dass sie einer Normalverteilung mit den Parametern \(\overline{x}\) und \(\sigma\) folgen.

Für das Beispiel nehmen wir \(\overline{x}=25\) und \(\sigma=3\) an. Schauen Sie sich genau an, wie die Funktion angewandt wird:

mw <- 25
sd <- 3
y_werte <- dnorm(x_werte, mw, sd)

Nun haben wir die Werte. Zur Überprüfung, ob es sich wirklich um eine Normalverteilung mit den Parametern handelt, können wir sie als Histogramm darstellen. Da die simulierten Werte ja einer theoretischen Normalverteilung entsprechen, müssen wir in der uns bereits bekannten Funktion geom_histogram im Paket ggplot2 definieren, dass der Plot als sog. Dichtefunktion dargestellt wird. Dies tun wir mittels der Spezifizierung afterstat(density) in den aesthetics. Für das Beispiel hier, plotten wir lediglich das Liniendiagram:

Liniendiagram

ggplot() +
  geom_line(aes(x=x_werte, y=y_werte), color="blue", size=1) +
  theme_bw() + 
  labs(title="Normalverteilung als Dichtefunktion")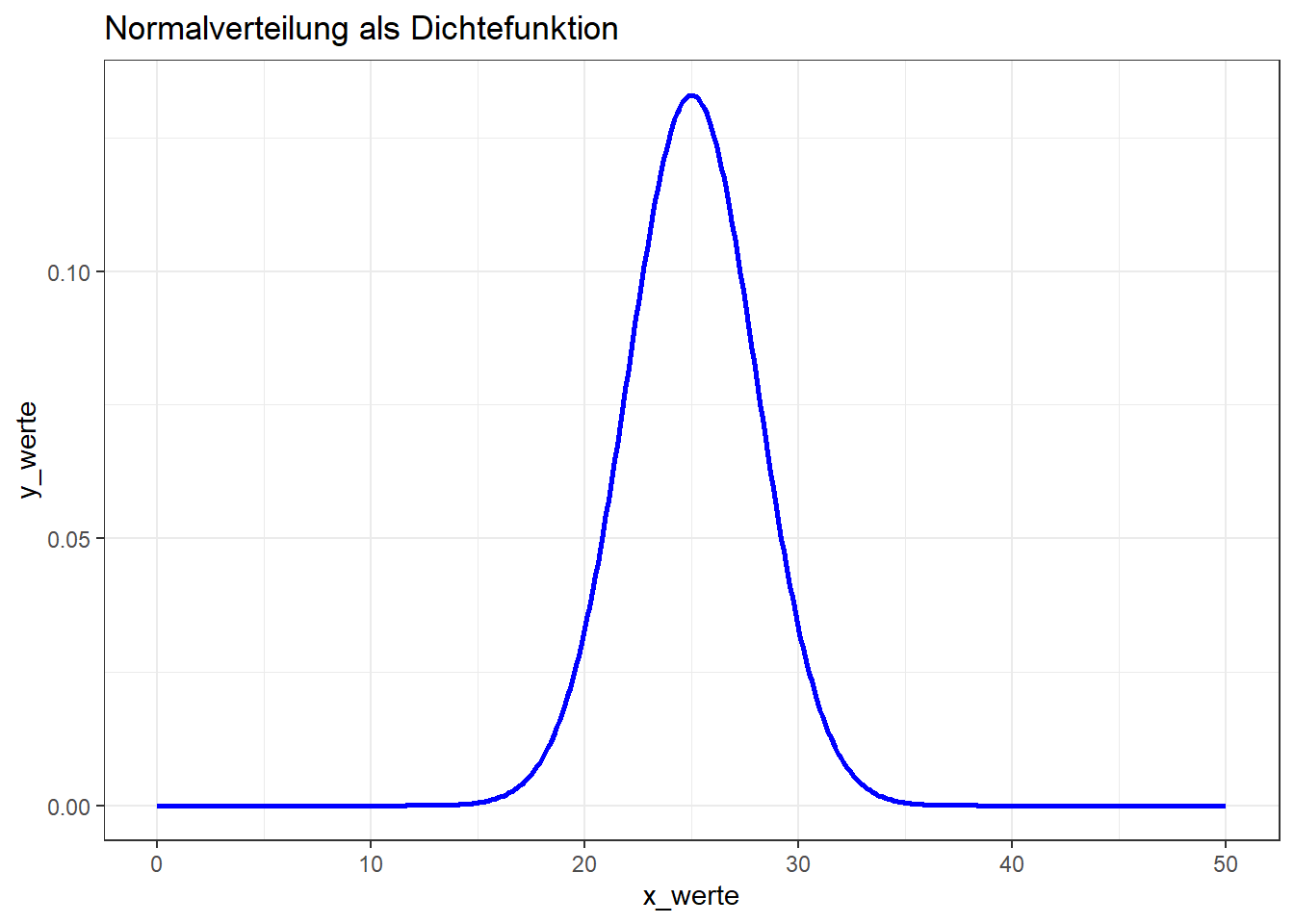

Das sieht gut aus! Zuletzt lernen wir noch, wie wir ein QQ-Diagram in R erstellen.

QQ-Diagram in R

Um dem Diagram einen Sinn zu geben, simulieren wir die Werte, die wir darstellen bzw. überprüfen wollen - nehmen wir also an, dass wir einen DataFrame haben, der in der ersten Spalte IDs von Studienteilnehmenden einer erfundenen Studie haben, und eine Spalte Groesse [cm] mit zufällig gewählten Körpergrößen haben:

df <- data.frame(ID=seq(1, 100, 1),
                 Groesse=round(rnorm(100, mean=1.78, sd=0.1),2))

head(df, 10)

   ID Groesse
1   1    1.83
2   2    1.62
3   3    1.62
4   4    1.92
5   5    1.82
6   6    1.81
7   7    1.88
8   8    1.79
9   9    1.72
10 10    1.74

ggplot(data=df, aes(sample=Groesse)) +
  stat_qq() +
  stat_qq_line() +
  theme_bw() + 
  labs(title="QQ-Plot und QQ-Line")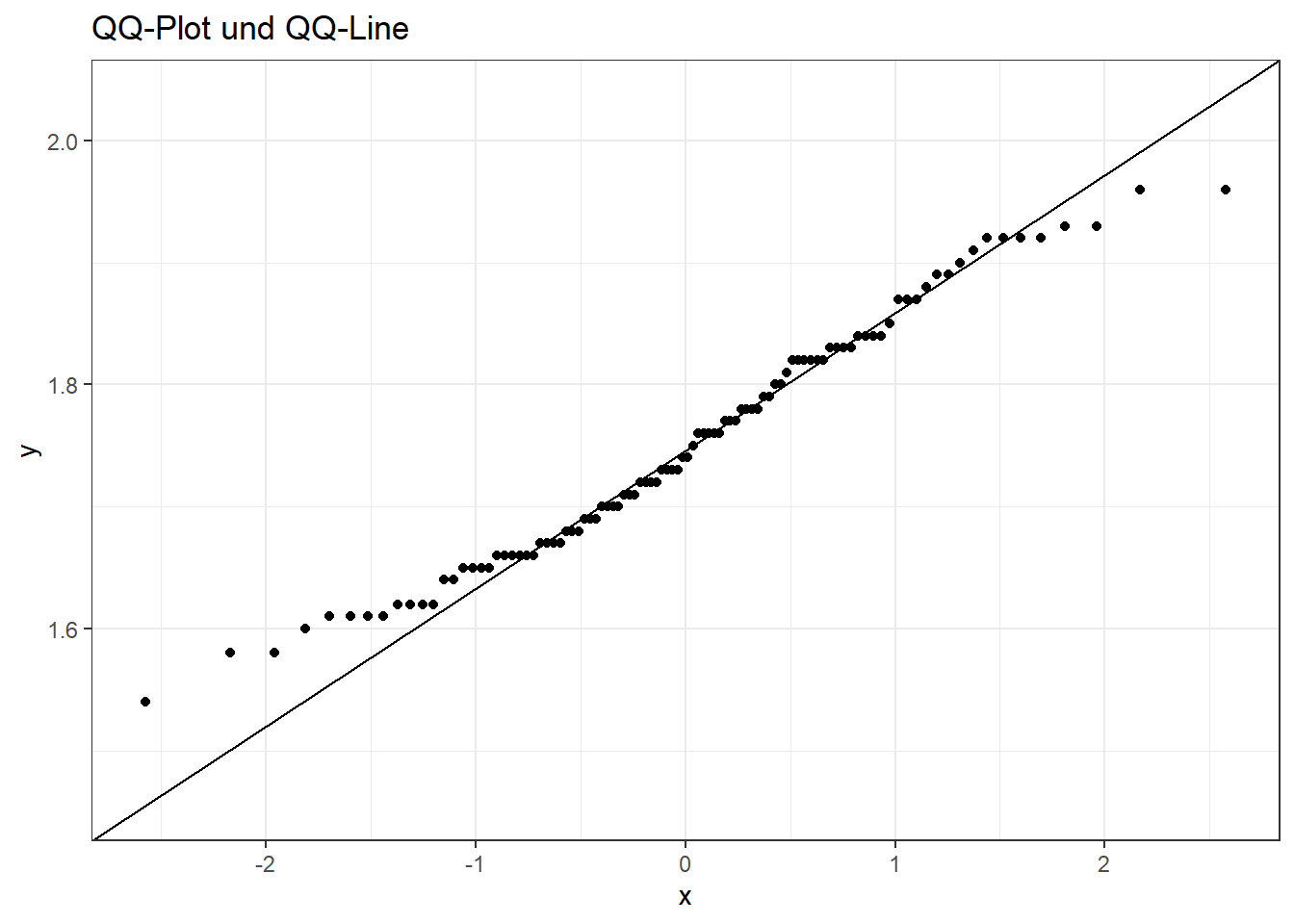

Zusätzliche Ressource: Warum die Normalverteilung so wichtig ist

Zum Abschluss empfehlen wir Ihnen dieses kurze Video, das auf einfache Weise erklärt, wofür wir die Normalverteilung in der Statistik nutzen und warum sie so zentral für viele statistische Verfahren ist: